파이썬 코드
https://github.com/JHWannabe/self-taught_machine_learning_code.git
6.1 군집 알고리즘
비지도 학습(Unsupervised Learning): 타깃이 없을 때 사용하는 머신러닝 알고리즘




히스토그램
- 값이 발생한 빈도를 그래프로 표시한 것
- 보통 x축이 값의 구간(계급), y축은 발생 빈도(도수)
평균값과 가까운 사진 고르기
3장에서 봤던 절댓값 오차를 사용
numpy의 abs() : 절댓값을 계산하는 함수 (ex. np.abs(-1) = 1)
군집(Clustering) : 비슷한 샘플끼리 그룹으로 모으는 작업
ㄴ 대표적인 비지도 학습 작업
클러스터(Cluster) : 군집 알고리즘에서 만든 그룹
6.2 k-평균
k-평균(k-means) 군집알고리즘 : 평균값을 자동으로 찾아줌
ㄴ 평균값이 클러스터의 중심에 위치하기 때문에 클러스터 중심(cluster center) 또는 센트로이드(centroid)라고 부름
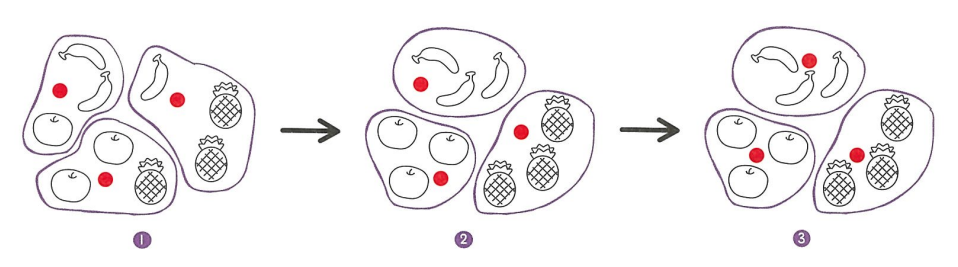
k-평균 알고리즘 작동 방식
- 무작위로 k개의 클러스터 중심을 정한다.
- 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정한다.
- 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경한다.
- 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복한다.
사이킷런으로 k-평균 모델 구현
KMeans 클래스
사이킷런의 k-평균 알고리즘은 sklearn.cluster 모듈 아래 KMeans 클래스에 구현되어 있음.
ㄴ 이 클래스에서 설정할 매개변수: 클러스터 개수를 지정하는 n_clusters

군집된 결과는 KMeans 클래스 객체의 labels_ 속성에 저장됨.
labels_ 배열의 길이 = 샘플의 개수
클러스터 중심
KMeans 클래스가 최종적으로 찾은 클러스터 중심은 cluster_centers_ 속성에 저장됨.
이 배열은 fruits_2d 샘플의 클러스터 중심이기 때문에 각 중심을 이미지로 출력하려면 100 x 100 크기의 2차원 배열로 바꿔야 함.
transform() 메서드 : 훈련 데이터 샘플에서 클러스터 중심까지 거리로 변환해 주는 메서드
최적의 k 찾기
k-평균 알고리즘의 단점 : 클러스터 개수를 사전에 지정해야 하는 것
엘보우(elbow) 방법
- 적절한 클러스터 개수를 찾기 위한 대표적인 방법
- 이너셔(inertia) : 클러스터 중심과 클러스터에 속한 샘플 사이의 거리의 제곱 합
ㄴ 클러스터에 속한 샘플이 얼마나 가깝게 모여 있는지를 나타낸 값
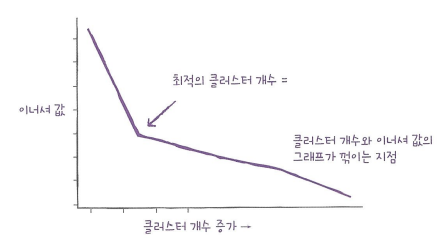
- 엘보우 방법은 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수를 찾는 방법.
- 클러스터 개수를 증가시키면서 이너셔를 그래프로 그래면 감소하는 속도가 꺽이는 지점이 있는데, 마치 팔꿈치 모양이어서 엘보우 방법이라 부름.

6.3 주성분 분석
차원과 차원 축소
- 차원(dimension) : 특성(feature, 데이터가 가진 속성)의 다른 용어
- 차원 축소: 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도 학습 모델의 성능을 향상시킬 수 있는 방법 (비지도 학습 작업 중 하나)
주성분 분석(PCA, Principal Component Analysis)
- 데이터에 있는 분산이 큰 방향을 찾는 것

(2, 1)의 벡터를 주성분이라고 한다.
주성분 벡터의 원소 개수 = 원본 데이터셋에 있는 특성 개수
원본 데이터는 주성분을 사용해서 차원을 줄일 수 있음.

s(4, 2)를 주성분에 직각으로 투영하면 1차원 데이터 p(4.5)로 변환할 수 있음.
첫 번째 주성분을 찾은 다음 이 벡터에 수직이고 분산이 가장 큰 다음 방향을 찾음. → 두 번째 주성분
일반적으로 주성분은 원본 특성의 개수만큼 찾을 수 있음.

PCA 클래스



주성분의 개수, 배열의 첫 번째 차원이 50이라는 것.
주성분을 그림으로 표현.

주성분을 찾았으므로 원본 데이터를 주성분에 투영하여 특성의 개수를 10,000개에서 50개로 줄일 수 있음.



설명된 분산(Explained Variance)
- 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값
- 총 분산 비율 : 분산 비율을 모두 더한 값


다른 알고리즘과 함께 사용하기
사이킷런의 LogisticRegression 모델과의 혼합.


원본 데이터인 fruits_2d를 사용하고, 로지스틱 회귀 모델에서 성능을 가늠하기 위해 cross_validate()로 교차 검증 수행.

PCA로 축소한 fruits_pca를 사용했을 때와 비교.

앞서 PCA 클래스를 사용할 때 n_componenets 매개변수에 주성분의 개수를 지정함.
→ 여기서도 원하는 설명된 분산의 비율을 입력할 수 있음.
PCA 클래스는 지정된 비율에 도달할 때까지 자동으로 주성분을 찾음.
설명된 분산의 50%에 달하는 주성분을 찾도록 PCA 모델을 만듦


원본데이터를 변경하고 교차검증 결과를 확인.


차원 축소된 데이터를 사용해 K-평균 알고리즘으로 클러스터 찾기




차원 축소의 장점
- 데이터셋의 크기를 줄일 수 있고 비교적 시각화하기 쉬움.
- 차원축소된 데이터를 지도 학습 알고리즘이나 다른 비지도 학습 알고리즘에 재사용하여 성능을 높이거나 훈련 속도를 빠르게 만들 수 있음.
'AI 입문 > Machine Learning' 카테고리의 다른 글
| 5장 - 트리 알고리즘 (0) | 2022.11.25 |
|---|---|
| 4장 - 다양한 분류 알고리즘 (0) | 2022.11.11 |
| 3장 - 회귀 알고리즘과 모델 규제 (1) | 2022.11.11 |


