4장 - 신경망 시작하기
분류와 회귀에서 사용하는 용어
- 샘플 또는 입력 : 모델에 주입될 하나의 데이터 포인트(data point)
- 예측 또는 출력 : 모델로부터 나오는 값
- 타깃 : 정답, 외부 데이터 소스에 근거하여 모델이 완벽하게 예측해야 하는 값
- 예측 오차 또는 손실 값 : 모델의 예측과 타깃 사이의 거리를 측정한 값
- 클래스 : 분류 문제에서 선택할 수 있는 가능한 레이블의 집합
- 레이블 : 분류 문제에서 클래스 할당의 구체적인 사례
- 참 값(ground-truth) 또는 에노테이션(annotation) : 데이터셋에 대한 모든 타깃. 일반적으로 사람에 의해 수집
- 이진 분류 : 각 입력 샘플이 2개의 배타적인 범주로 구분되는 분류 작업
- 다중 분류 : 각 입력 샘플이 2개 이상의 범주로 구분되는 분류 작업. 예를 들어 손글씨 숫자 분류
- 다중 레이블 분류: 각 입력 샘플이 여러 개의 레이블에 할당될 수 있는 분류 작업
- 스칼라 회귀 : 타깃이 연속적인 스칼라 값인 작업. 예를 들어 주택 가격 예측
- 벡터 회귀 : 타깃이 연속적인 값의 집합인 작업. 예를 들어 연속적인 값으로 이루어진 벡터
- 미니 배치 또는 배치 : 모델에 의해 동시에 처리되는 소량의 샘플 묶음(일반적으로 8~128개 사이).
- ㄴ 샘플 개수는 GPU 메모리의 할당이 용이하도록 2의 거듭제곱으로 하는 경우가 많음. 훈련할 때 미니 배치마다 한 번씩 모델의 가중치에 적용할 경사 하강법 업데이트 값을 계산.
4.1 이진 분류 문제
4.1.1 IMDB 데이터셋
- 인터넷 영화 데이터베이스(Internet Movie Database) : training data - 25,000, test data - 25,000
ㄴ 원본 텍스트 데이터를 전처리하는 방법은 11장에서..
num_words=10000 매개변수는 훈련 데이터에서 가장 자주 나타나는 단어 1만 개만 사용한다는 의미
재미 삼아 리뷰 데이터 하나를 원래 영어 단어로 바꾸는 방법

4.1.2 데이터 준비
리스트를 텐서로 바꾸는 두 가지 방법
- 같은 길이가 되도록 리스트에 패딩(padding)을 추가하고 (samples, max_length) 크기의 정수 텐서로 변환한다. 그다음 이 정수 텐서를 다룰 수 있는 layer로 신경망을 시작한다. (Embedding Layer를 말하며, 나중에 자세히 다룸)
- 리스트를 멀티-핫 인코딩(multi-hot encoding)하여 0과 1의 벡터로 변환한다. 예를 들어 [8,5]를 인덱스 8과 5의 위치는 1이고 기외는 모두 0인 10,000차원의 벡터로 각각 변환한다. 그다음 부동 소수점 벡터 데이터를 다룰 수 있는 Dense Layer를 신경망의 첫 번째 층으로 사용한다.

4.1.3 신경망 모델 만들기
입력데이터가 벡터고 레이블은 스칼라(1 또는 0).
Dense 층을 쌓을 때 두 가지 중요한 구조상의 결정이 필요
- 얼마나 많은 Layer를 사용할 것인가?
- 각 Layer에 얼마나 많은 unit을 둘 것인가?
5장에서 이런 결정을 하는 데 도움이 되는 일반적인 원리를 배움.
예시로 다음 구조를 따른다.
- 16개의 unit을 가진 2개의 중간 Layer
- 재 리뷰의 감정을 스칼라 값의 예측으로 출력하는 세 번째 Layer


Dense layer에 전달한 첫 번째 매개변수는 Layer의 unit 개수이며, Layer가 가진 표현 공간의 차원이다.
16개의 unit이 있다는 것은 가중치 행렬 W의 크기가 (input_dimension, 16)이라는 뜻
표현 공간의 차원 : 모델이 내재된 표현을 학습할 때 가질 수 있는 자유도
ㄴ unit을 늘리면 모델이 더욱 복잡한 표현을 학습할 수 있지만 계산 비용이 커지고 원하지 않는 패턴을 학습할 수도 있음.
중간층은 활성화 함수로 relu를 사용하고 마지막 층은 확률을 출력하기 위해 시그모이드 활성화 함수를 사용한다.
ㄴ 활성화 함수는 무엇이고 왜 필요한가?
ㄴ 활성화 함수가 없다면 Dense 층은 선형적인 연산인 점곱과 덧셈 2개로 구성된다. 그러므로 이 층은 입력에 대한 선형 변환(affine 변환)만 학습할 수 있다. 이 층의 가설 공간은 입력 데이터를 16차원의 공간으로 바꾸는 가능한 모든 선형 변환의 집합이다. 이런 가설 공간은 매우 제약이 많으며, 선형 층을 깊게 쌓아도 여전히 하나의 선형 연산이기 때문에 층을 여러 개로 구성하는 장점이 없다.
마지막으로 손실 함수와 옵티마이저를 선택해야 한다.
손실 함수는 이진 분류 문제이고 모델의 출력이 확률이기 때문에 binary_crossentropy 손실이 적합하다. 이 함수가 유일한 선택은 아니고 mean_squared_error도 사용할 수 있다. 확률을 출력하는 모델을 사용할 때는 crossentropy가 최선의 선택이다.
ㄴ crossentropy는 정보 이론 분야에서 온 개념으로 확률 분포 간의 차이를 측정한다. 여기에서는 원본 분포와 예측 분포 사이를 측정한다.
옵티마이저는 rmsprop을 사용한다. 이 옵티마이저는 일반적으로 거의 모든 문제에 기본 선택으로 좋다.

4.1.4 훈련 검증




4.1.5 훈련된 모델로 새로운 데이터에 대해 예측하기
4.1.6 추가 실험
4.1.7 정리
4.2 다중 분류 문제
4.2.1 로이터 데이터셋
- 1986년 로이터에서 공개한 짧은 뉴스 기사와 토픽의 집합인 로이터 데이터셋 : 46개의 토픽, 각 토픽은 훈련 세트에 최소한 10개의 샘플을 갖고 있음


4.2.2 데이터 준비
- 데이터를 벡터로 변환한다.

레이블을 벡터로 바꾸는 방법 2가지
- 레이블의 리스트를 정수 텐서로 변환하는 것
- 원-핫 인코딩(one-hot encoding) : 범주형 데이터에 널리 사용되어 범주형 인코딩(categorical encoding)이라고도 함.

4.2.3 모델 구성
- 이진 분류와 다른 점은 출력 클래스의 개수가 2에서 46개로 늘어난 것. (출력 공간의 차원이 커짐)

이 구조에서 주목해야 할 점 2가지
- 마지막 Dense 층의 크기가 46 → 각 입력 샘플에 대해 46차원의 벡터를 출력한다는 뜻.
- 마지막 층에 softmax 활성화 함수가 사용됨. 각 입력 샘플마다 46개의 출력 클래스에 대한 확률 분포를 출력.

4.2.4 훈련 검증




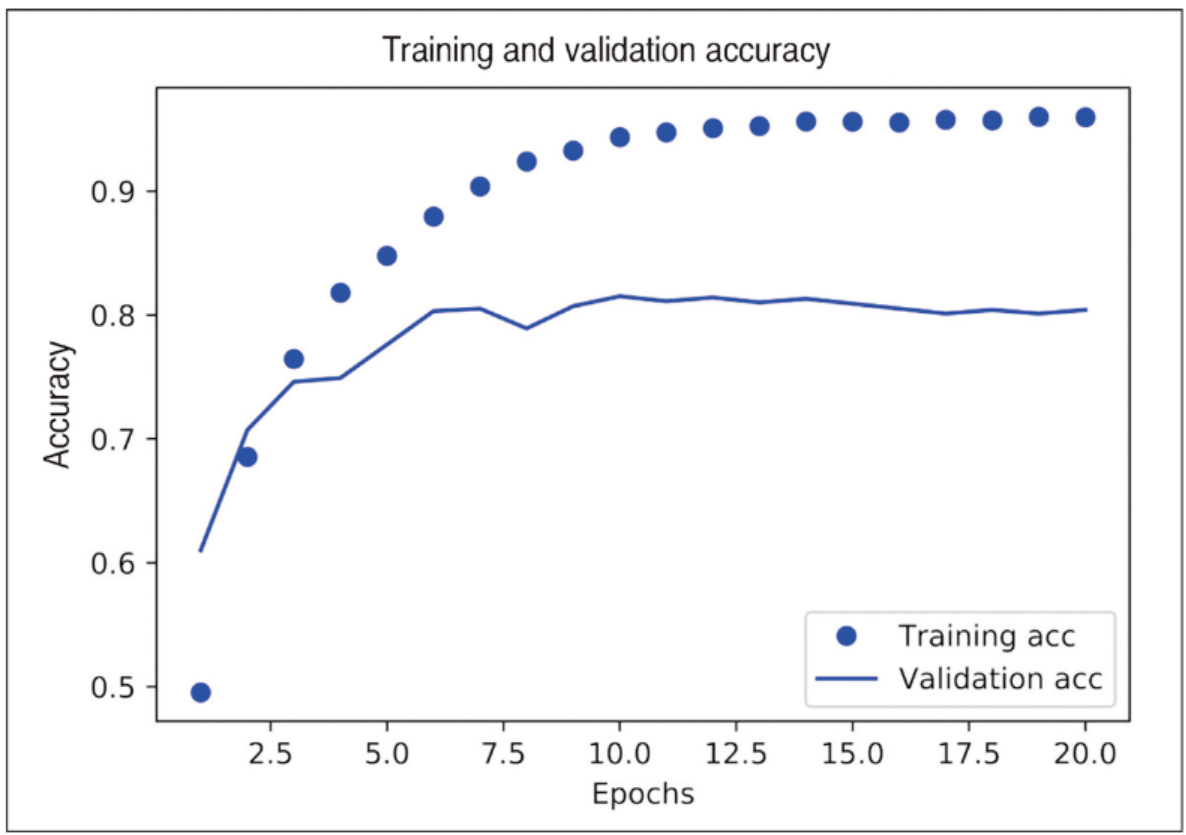
4.2.5 새로운 데이터에 대해 예측하기
4.2.6 레이블과 손실을 다루는 다른 방법
4.2.7 충분히 큰 중간층을 두어야 하는 이유
46차원보다 훨씬 작은 중간층을 두면 정보의 병목이 어떻게 나타나는지 확인한다.

검증 정확도의 최고 값은 71%로 8% 정도 감소되었다. 이런 손실의 원인 대부분은 많은 정보를 중간층의 저차원 표현 공간으로 압축하려고 했기 때문이다.
4.2.8 추가 실험
4.2.9 정리
4.3 회귀 문제
4.3.1 보스턴 주택 가격 데이터셋
- 1970년 중반 보스턴 외곽 지역의 범죄율, 지방세율 등의 데이터가 주어졌을 때 주택 가격의 중간 값을 예측한다.
ㄴ 데이터 포인트가 506개로 비교적 개수가 적고 404개는 훈련 샘플로, 102개는 테스트 샘프로 나뉘어 있음.

4.3.2 데이터 준비

테스트 데이터를 정규화할 때 사용한 값이 훈련 데이터에서 계산한 값임을 주목!
머신 러닝 작업 과정에서 절대로 테스트 데이터에서 계산한 어떤 값도 사용해서는 안됨!
데이터 정규화처럼 간단한 작업조차도...
4.3.3 모델 구성
샘플 개수가 적기 때문에 64개의 unit을 가진 2개의 중간층으로 작은 모델을 구성하여 사용한다. 일반적으로 훈련 데이터의 개수가 적을수록 과대적합이 더 쉽게 일어나므로 작은 모델을 사용하는 것이 과대적합을 피하는 방법이다.

이 모델의 마지막 층은 하나의 유닛을 가지고 있고 활성화 함수가 없다.(선형 층)
이것이 전형적인 스칼라 회귀를 위한 구성이다.(하나의 연속적인 값을 예측하는 회귀)
활성화 함수를 적용하면 출력 값의 범위를 제한하게 된다.
이 모델은 mse 손실 함수를 사용하여 컴파일한다. 이 함수는 평균 제곱 오차(mean squared error)의 약어로 예측과 타깃 사이의 거리의 제곱이다. 회귀 문제에서 널리 사용되는 손실 함수이다.
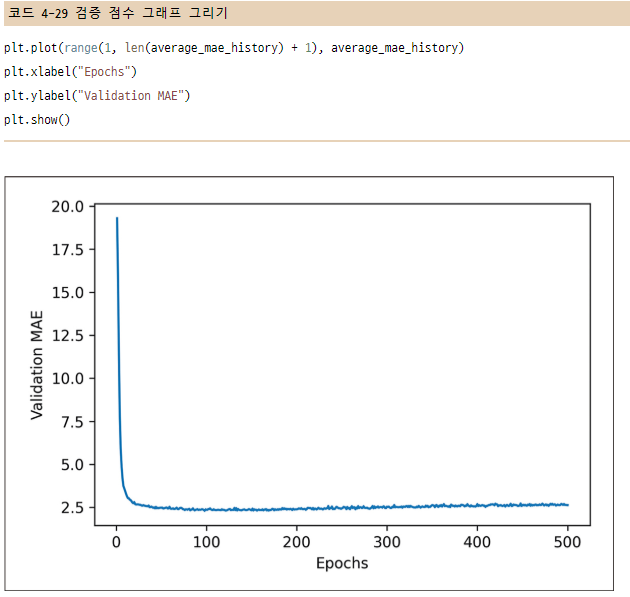
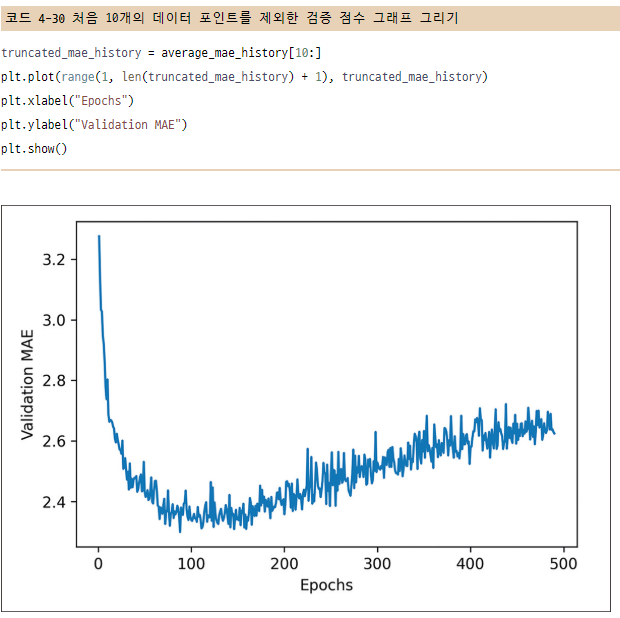
훈련하는 동안 모니터링을 위해 새로운 지표인 평균 절대 오차(Mean Absolute Error, MAE)를 측정한다. 이는 예측과 타깃 사이 거리의 절댓값이다.
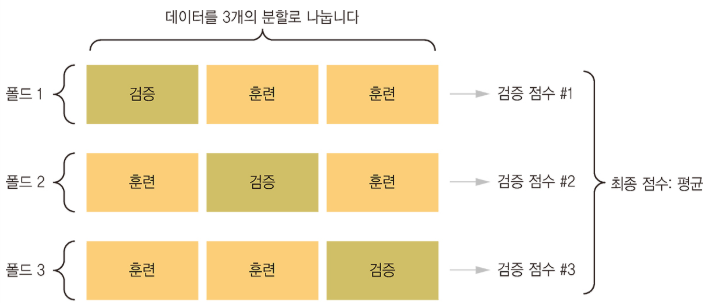
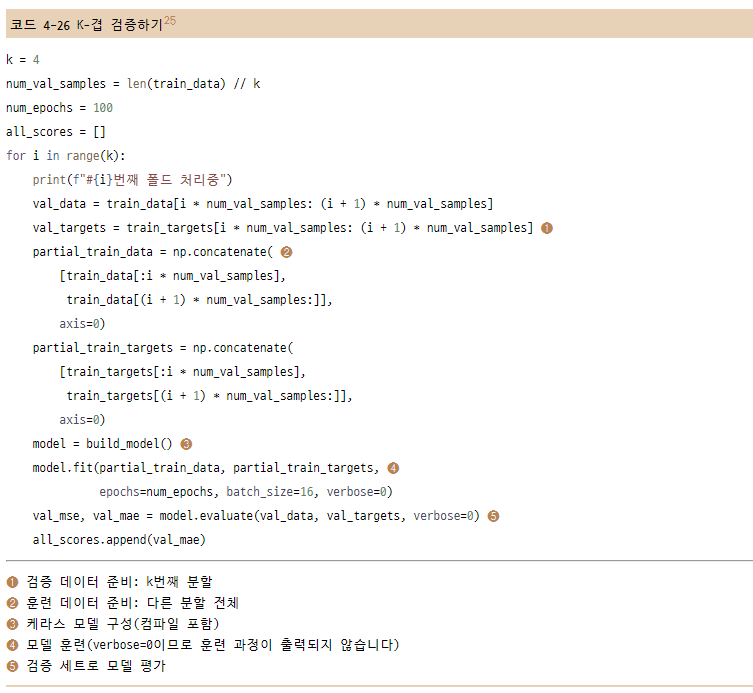
4.3.4 K-겹 검증을 사용한 훈련 검증
매개변수들을 조정하면서 모델을 평가하기 위해 이전 예제에서 했던 것처럼 데이터를 훈련 세트와 검증 세트로 나눈다.
데이터 포인트가 많지 않기 때문에 검증 세트도 매우 작아진다. 결국 검증 세트와 훈련 세트로 어떤 데이터 포인트가 선택되었는지에 따라 검증 점수가 크게 달라진다. 즉, 검증 세트의 분할에 대한 검증 점수의 분산이 높다. 이렇게 되면 모델을 신뢰 있게 평가할 수 없다.
이럴 때 사용하는 방법이 K-fold cross-validation을 사용하는 것이다.